- cross-posted to:
- memes@lemmy.world
- cross-posted to:
- memes@lemmy.world
Explanation (which might be wrong, since I’m writing this after banging my head against a wall. Please do correct me if I’m wrong):
In regular numbering systems (i.e., decimal), we exhaust all 10 digits (0–9) before we reach two-digit numbers. The first number to require 3 digits is 10². The first to use 4 is 10³, and so on.
In music intervals, there is no “0”. The interval c’–c’, for instance, is called a prime (1). This has the funny consequence that moving by a fifth and then by a fourth doesn’t land you on the ninth, but the octave (8). Moving by an octave and then another octave gets you to the 15th, not the 16th.
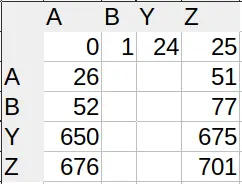
In Excel, shit hits the fan when you need to convert column names (A, B, C…) to numbers (0, 1, 2…). Since we use 26 characters as our ‘digits’, we’re in the hexavigesimal system. Knowing what I told you in the first paragraph, you’d expect the first double-digit column (AA) to be 26. And you’re right.
However, when do we need 3 digits? Which column is column AAA? A sane person would say it’s 26², so 676. Ha! No. Column number 676 is actually ZA. What gives? Well, we only ditch the zero for single digit numbers. All subsequent columns actually use 27 different characters, the ‘empty character’ being one of them. That’s where we get the ‘single digit’ – there actually is a second digit, only it’s empty.
So the column AAA actually has index 702, or 26×27. Which index does the column AAAA have? 26×27². The system of adding powers of the base works, only we changed bases midway through.
You can see the lopsidedness in the index lookup table (I’m not displaying all characters for brevity). Sane number systems have square tables. Excel’s is 26×27 (shown are 4×5).

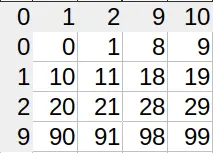
I’m a bit too tired and tipsy to fully wrap my head around this but I’m just as furious as you are!
This has the funny consequence that moving by a fifth and then by a fourth doesn’t land you on the ninth, but the octave (8). Moving by an octave and then another octave gets you to the 15th, not the 16th.
This is worded confusingly. The reason for this is simply because you include the base note when you start counting, so if you stop midway and stack another interval on top, you have to account for that stop because it decreases the total travel distance by one.
This is done to actually increase consistency. If you start at c1 and move up an octave and then move up another octave, you stop at c3 which is logical. So you either move 2 octaves or one 15th because 2*8-1 = 15.
This is a very fun implicit question!
First, in decimal, there are 10 symbols: 0-9. When we count from 0 to 9, the next number is 10, not 00 (which is equivalent to 0).
In base 26, there are 26 symbols (A-Z). If one wanted to use these symbols in the same way, A would be equivalent to 0, so 26 is represented by BA, not AA. However, if AA is not the same as A, then we can represent 26 as AA instead of BA.
Basically, in our typical numbering system, the leading digit can’t be 0, so there are 9×10 possible two digit numbers, and 10 possible single digit numbers. However, if the first digit can be 0, meaning, for example, if 03 is not the same as 3, there are 10×10 possible two digit numbers. This second approach is what excel and google sheets use. Column A is not the same as column AA. Hence, you start with single digit column numbers (A-Z). Then you move to two digit column numbers (AA-ZZ), of which there are 26². The last column before triple digits is column 26+26²=702. The first triple digit column number is 26+26²+1=703. Neat!
Comparing this to our system, the first 2 digit number is 10¹=10. The first 3 digit number is 10²=100. The first 4 digit number is 10³=1000.
People are focusing on the Excel part, I’ll focus on the maths.
I wish our societies picked base-12 instead of base-10. Divisions in base-12 give you repeating digits less often, and being able to split exactly by 3, 6, 9 and 12₁₀=10₁₂ is far more useful than doing it for 5 and 10₁₀=A₁₂.
Plus 4chan would stop arguing if 0.999… = 1. It would argue instead if 0.BBB… = 1.I got confused by your explanation, I think partly because of conversion to decimal without specifying whether column A is 0 or 1. To match the row numbering system, I’d assume it’s 1, but mathematically it might be easier to analyze if it starts at 0.
Here’s my attempt to understand it better.
How many spreadsheet rows are 1 digit? 1-9, that’s 9 rows.
How many rows are 2 digit? 10-99, that’s 90 rows.
How many rows are 3 digit? 100-999, that’s 900 rows.
The pattern is: there are 9 × 10^(d-1) rows that are d digits.
Now for columns. How many columns are 1 letter? A-Z, that’s 26.
How many columns are 2 letters? AA-ZZ, that’s 26².
How many columns are 3 letters? AAA-ZZZ, that’s 26³.
The pattern is: there are 26^d columns that are d letters.
Now let’s look at running totals. How many rows are at most 2 digits? 9 + 90 = 99
How many rows are at most 3 digits? 99 + 900 = 999
The pattern is: 10^d - 1 rows are at most d digits.
How many columns are at most 2 letters? 26 + 26² = 26×(1 + 26) = 26×27
How many columns are at most 3 letters? 26×27 + 26³ = 26×(27 + 26²)
Alternatively: 26 + 26² + 26³
I can’t find a more compact way of writing it.
The pattern is: Σ26^k (k from 1 to d) columns are at most d letters
I might be wrong but I don’t think this matches up with what you said, which is 26×27^(d-2) + c (where c is some constant for converting between what we’re trying to measure, probably 1 or -1)
Wait duh, it’s a geometric series. I’m a little out of touch there but online resources are aplenty, so the pattern is:
There are (26^d - 1)×26/25 columns are are at most d letters.
For Hardcore geeks






